Lögmálið um sinus og kósínus getur verið erfitt að skilja, en það snýst allt um hliðar og horn (hornpunkta) og hlutfallstengsl þeirra. Þegar krakkar hafa náð tökum á grunnjöfnunum geta þau notað upplýsingarnar sem gefnar eru til að reikna út magn sem vantar. Trigonometry á við um margs konar raunverulegar starfsgreinar og leiki sem sýna þessa stöðu ofarlega í skemmtilegum stuðli nemenda. Sem fljótleg áminning notar Sines-lögmálið SSA og AAS en Cosines-lögmálið notar SSS eða SAS. Vertu meðvituð um að nemendur þurfa að nota reiknivélar fyrir þetta stærðfræðistig.

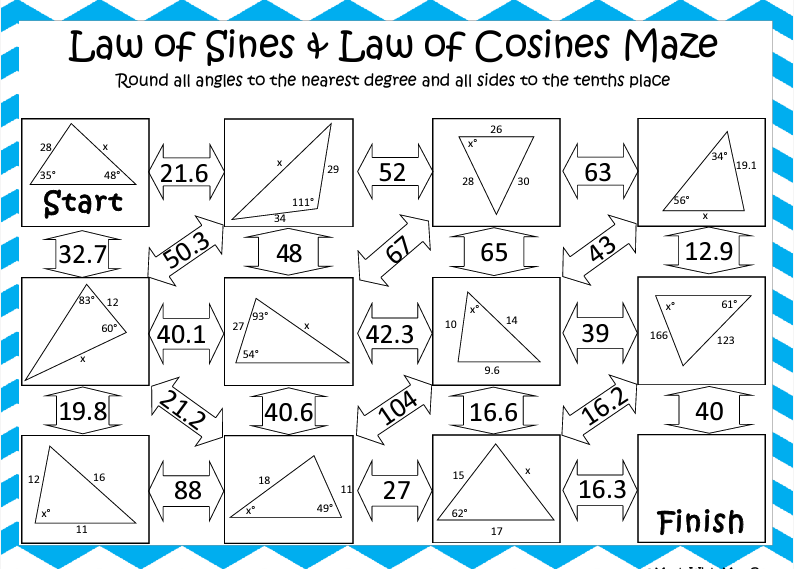
1. Völundarhús

Áskoraðu nemendur með þessu flókna völundarhúsi. Þeir verða að reikna út þær hliðar sem vantar og/eða hornmælingar til að vita hvaða leið á að fara í völundarhúsið. Þetta skapar auka skemmtun fyrir erfiðar stærðfræðijöfnur.

2. PowerPoint hlaup

Nemendum er skipt í lið fyrir þetta Powerpoint hlaup til að svara tíu spurningum. Leysa þarf og sannreyna hverja spurningu áður en hægt er að fara yfir í næsta verkefni. Tilnefna nokkra krakka til að vera „hliðverðir“ sem sannreyna rétt svör. Hvaða lið vinnur?

3. Litun eftir kóða

Þetta vinnublað skorar á nemendur að nota lögmálin tvö til að leysa hina ýmsu þríhyrninga. Krakkarnir passa síðan svörin við ákveðna liti til að skreyta myndina. Þegar þeir eru komnir með litasamsvörun geta þeir litað tiltekinn hluta myndarinnar.

4.Geogebra

Starfsemi í Geogebru gerir nemendum kleift að sjá fyrir sér lögmál sinus. Mismunandi þríhyrningar búa til af nemendum þegar þeir færa punkta um skjáinn. Sex gildi hlutanna í þríhyrningnum breytast þegar punktarnir hreyfast. Það eru margir möguleikar til að skoða!

5. MapQuest

Skoðaðu bæinn þinn með því að nota MapQuest. Gefðu krökkunum gráðuboga, kort og leiðbeiningarnar. Þeir búa til þríhyrninga með því að nota aðeins nokkrar tilteknar mælingar og reikna út fjarlægðir milli staða á kortinu. Þeir þurfa að vera nákvæmir með mælingar til að finna réttar fjarlægðir.

6. Sólúr

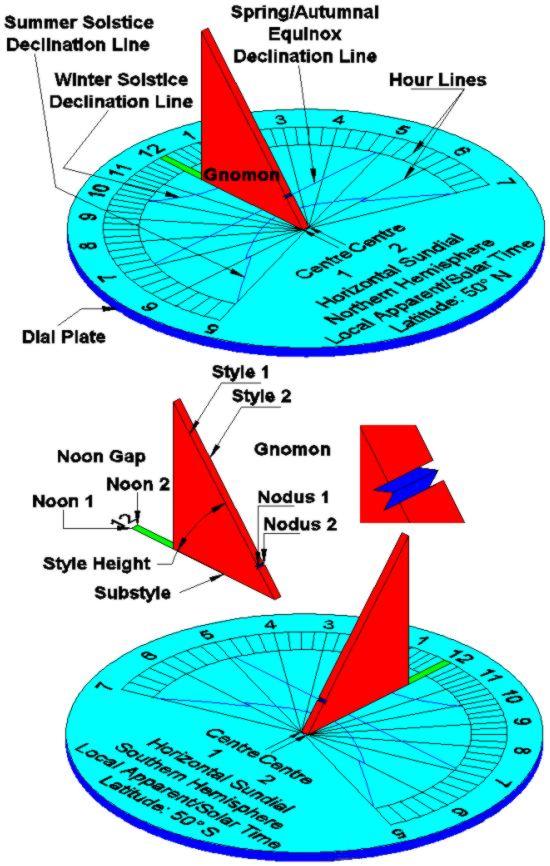
Nemendur æfa sig í að mæla þríhyrninga til að reikna út lengd skalaþríhyrninga til að reikna út hæð gnomonsins á sólúrunum sínum. Þeir munu nota hæð sólar og skuggalengd á mismunandi breiddargráðum til að finna út lengd stílsins.

7. Finndu fölsunina

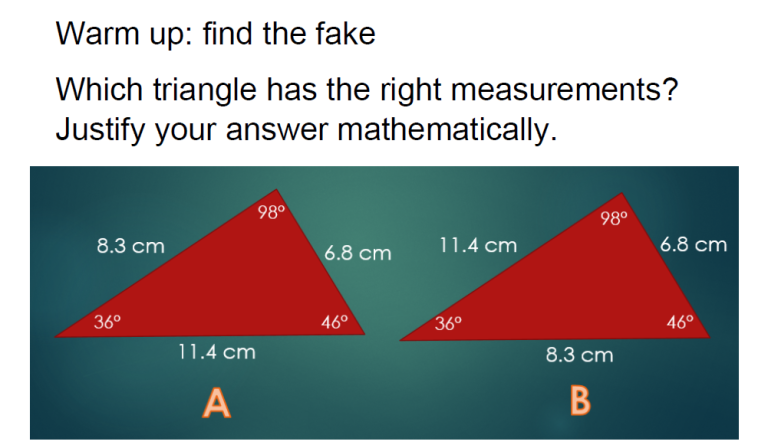
Við hvert horn, láttu nemendur ímynda sér að hvert horn sé vasaljósageisli sem vísar á gagnstæðan vegg. Hver myndi búa til hringinn með stærsta þvermálið á veggnum á móti? Stærsta hornið skapar stærsta þvermálið, svo nemendur munu að lokum uppgötva að B er falsað.

8. Ruslbolti

Einföld ruslafata og pappírsbútur búa til hópútreikninga. Krakkar leysa vandamál og ganga úr skugga um að þau séu rétt hjá þér. Ef rétt er, fá þeirtækifæri til að skora stig með því að búa til körfu – settu límbandslínur á gólfið til að gefa til kynna 1- og 2-punkta línur.

9. Scavenger Hunt

Búðu til röð orðadæma og settu þau um herbergið. Nemendur verða að leysa verkefnin og passa rétt svör við „fyrra svar“ sem sett er á hvert nýtt verkefni. Ef það er gert á réttan hátt ættu þeir að klára öll verkefni, safna bréfum á leiðinni til að svara gátu.

10. Smágolf

Kannaðu hornafræði með þessum gagnvirka minigolfleik. Krakkar verða að reikna út svör með sinus- og kósínushlutföllum til að geta spilað þennan skemmtilega golfleik almennilega. Þetta gefur flókinni stærðfræði alvöru snúning og gerir krökkum kleift að sjá forritið til að skemmta sér úti.

11. Pile-Up

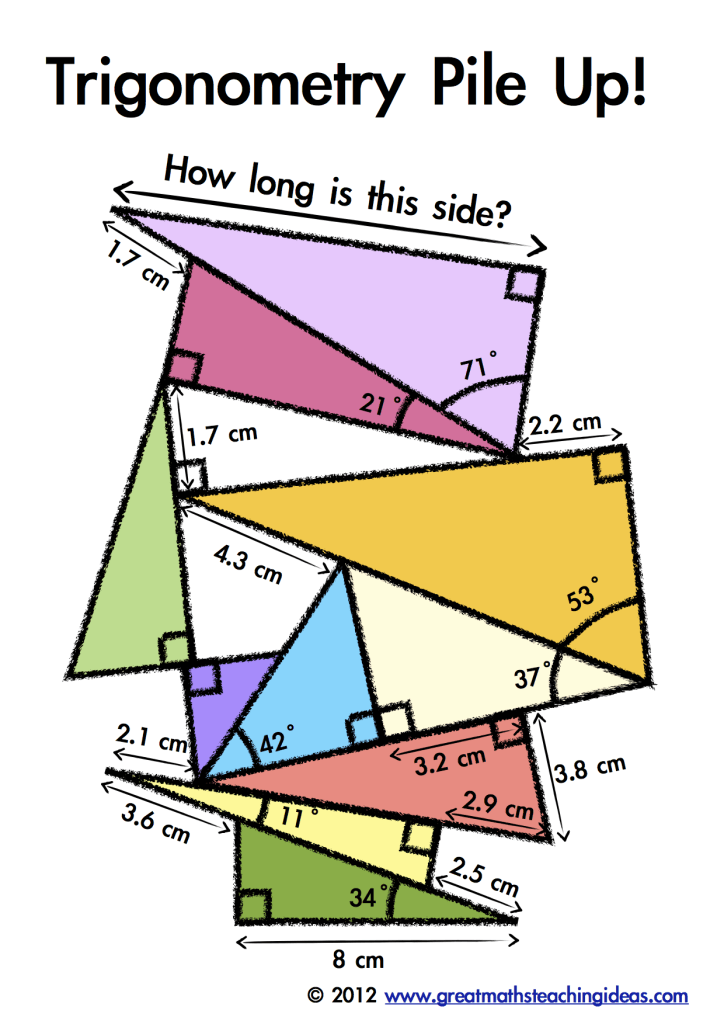
Krakkarnir leysa þessa krefjandi þraut með því að nota hornafræðireglur, þar á meðal sinus og kósínus. Þeir verða að nota upplýsingarnar sem gefnar eru til að reikna út hornin og hliðarlengdirnar sem vantar. Það mun taka mörg skref en mun tæla krakka til að búa til sína eigin hrúgu sem aðrir geta leyst.

12. Trig River

Nemendur munu beita raunverulegri þekkingu til að reikna út fjarlægð árinnar. Þeir munu einnig vinna með umbreytingu eininga og læra hvernig verkfræðingar nota hornafræði í raunveruleikanum. Gefðu krökkunum vinnublaðið, gráðuboga og streng til að áætla og reikna út vegalengdir.

13. ZenStærðfræði

Láttu nemendur búa til línur á hvítan pappír til að búa til 10 auða hluta. Reiknaðu síðan svörin sem vantar á hvern þríhyrning og taktu þau saman við samsvarandi mynstur. Notaðu að lokum mynstrið til að fylla út í eitt af auðu rýmunum á teikningunni.

14. Rocket Angles

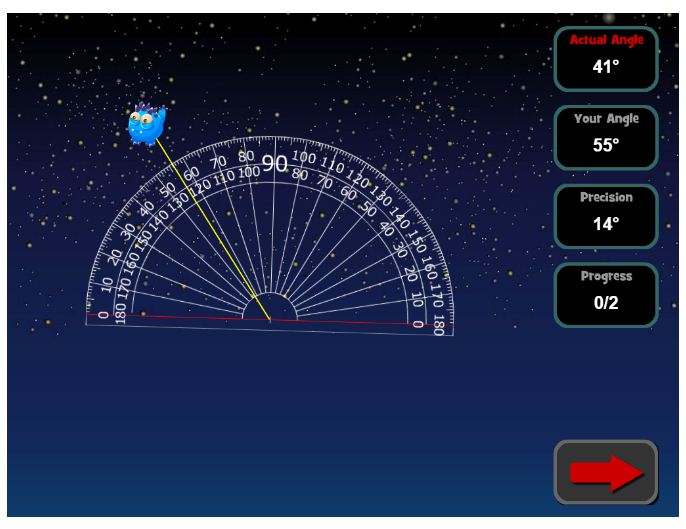
Krakkarnir spreyta sig sem eldflaugaskipstjórar í þessum gagnvirka netleik. Þeir munu reikna út hornin sem vantar til að finna geimverur í geimnum. Hver nemandi þarf gráðuboga til að reikna út horn og form.

15. Angry Birds

Trúðu það eða ekki, Angry Birds hjálpar krökkum að sjá fyrir sér þau sjónarhorn sem þarf til að skjóta niður fugla. Þeir munu læra hornafræðireglur með því að sjá fyrir sér ákjósanlegasta skothornið til að ná skotmarki sínu. Af hverju ekki að bæta við aukaeiningu með því að taka með gráðuboga og láta þá bera kennsl á þríhyrninga?

16. Atvinna Ímyndunarafl

Látið nemendur kanna notagildi hornafræði í ýmsum starfsgreinum. Hugsaðu um hvaða störf myndu nota þríhyrninga og krefjast útreikninga vegalengda. Láttu síðan krakka gera rannsóknir til að staðfesta spár sínar.

17. Búðu til þitt eigið

Áskoraðu krakka til að búa til sín eigin krefjandi orðavandamál og láttu myndskreytingar fylgja með til að sýna raunveruleg forrit. Láttu þá leysa vandamálið sérstaklega og skora svo á aðra að finna svarið eða leysa vandamálið og búa til veggspjald til að sýnaþekkingu þeirra.

18. Trigonik

Styðjið hreyfifræðilega nemendur með þessu flókna og skemmtilega borðspili. Tveir leikmenn mætast til að ná tvíburamerkjunum sínum í gegnum spilaborðið með því að kasta teningum og leysa vandamál. Teningarnir eru með ýmsir SIN og COS valmöguleikar, þar sem leikmenn staðsetja tákn sín meðfram hring.

19. Punktur-til-punktur

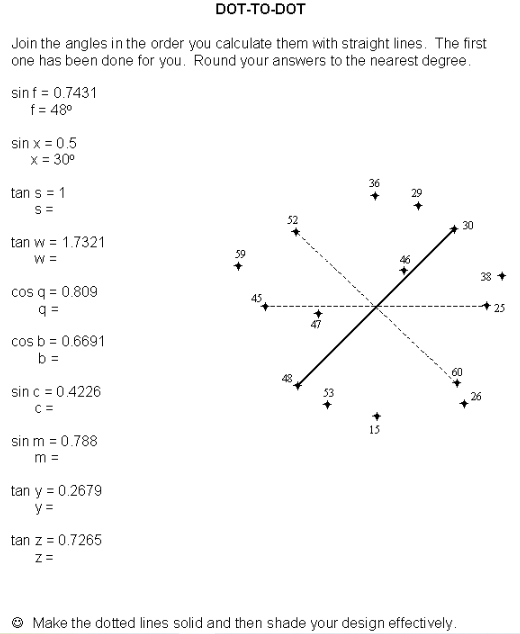
Notaðu þessa skapandi vandamálahugmynd til að uppfæra gamla skólann punkt-til-punkt. Krakkar verða að finna út svörin við mörgum hornafræðilegum vandamálum til að finna hvaða tvo línuhluta þeir eiga að tengja næst á leyndardómsgrafinu sínu.

20. 3D útreikningar

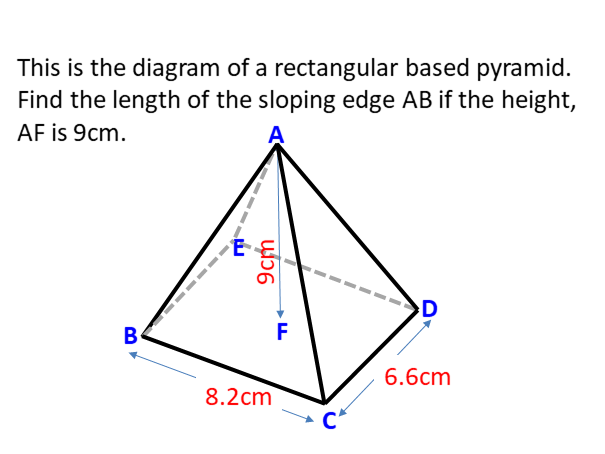
Frekari nemendur geta byrjað að sjá stærðfræði í þrívíddarformum. Unnið með þessi vandamál til að sýna fram á stækkaða útgáfu af hornafræði með því að nota lögmál sinus og kósínus. Krakkar þurfa að ákvarða horn og hliðarmælingar sem vantar til að leysa þrívíddarformið.

21. Raunveruleg myndbönd

Hlustaðu á vinsæla fagmenn í ýmsum störfum ræða hvernig þeir nota stærðfræði daglega í starfi sínu. Þá geta krakkar reynt fyrir sér í þessum netleikjum og vandamálum. Frá stærðfræði í körfubolta til stærðfræði í tæknibrellum, krakkar verða undrandi yfir öllum raunverulegum forritum námsins!

22. Sýndaraðgerðir

Skoðaðu ótrúlegar áskoranir sem Landsbókasafn sýndaraðgerða býður upp á. Með mörgumtilboð fyrir mismunandi stig, þessir leikir munu hjálpa krökkum að sjá stærðfræði fyrir sig á nýjan hátt og vinna með vandamálin, þar á meðal að mæla fjarlægð milli heimsborga.