Das Sinus- und Kosinusgesetz kann schwer zu verstehen sein, aber es geht um Seiten und Winkel (Scheitelpunkte) und ihre proportionalen Beziehungen. Sobald die Kinder die grundlegenden Gleichungen beherrschen, können sie die gegebenen Informationen verwenden, um fehlende Größen zu berechnen. Trigonometrie findet in einer Vielzahl von realen Berufen Anwendung, und Spiele, die dies zeigen, stehen bei den Schülern ganz oben auf dem Spaßquotienten. Als schnelleZur Erinnerung: Für das Sinusgesetz werden SSA und AAS verwendet, für das Kosinusgesetz SSS oder SAS. Beachten Sie, dass die Schüler für diese Mathematikstufe einen Taschenrechner benötigen.

1. die Irrgärten

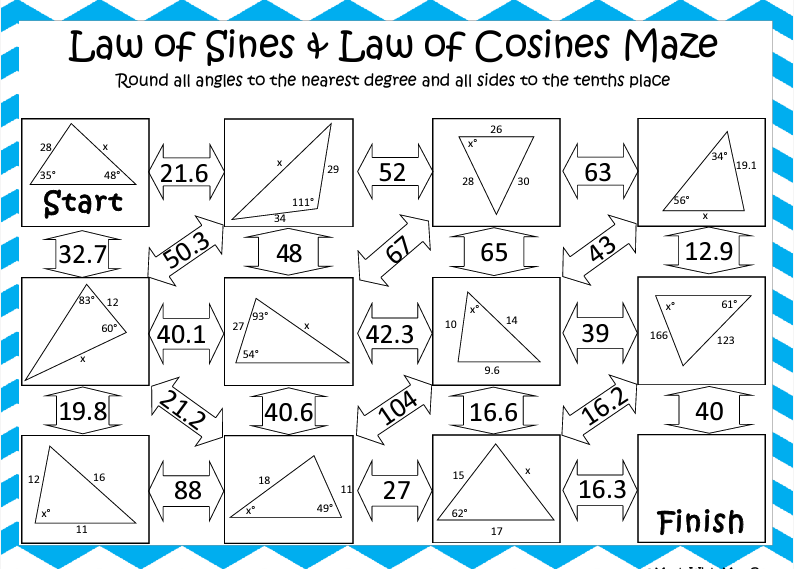
Fordern Sie die Schüler mit diesem komplizierten Labyrinth heraus. Sie müssen die fehlenden Seiten und/oder Winkelmaße berechnen, um zu wissen, welchen Weg sie im Labyrinth gehen müssen. Dies schafft ein zusätzliches Element des Spaßes für knifflige mathematische Gleichungen.

2) PowerPoint-Rennen

Die Schülerinnen und Schüler werden für dieses Powerpoint-Rennen in Teams eingeteilt, um zehn Fragen zu beantworten. Jede Frage muss gelöst und überprüft werden, bevor sie zum nächsten Problem übergehen können. Bestimmen Sie mehrere Kinder als "Torwächter", die die richtigen Antworten überprüfen. Welches Team wird gewinnen?

3. die Einfärbung nach Code

Dieses Arbeitsblatt fordert die Schüler auf, die beiden Gesetze anzuwenden, um die verschiedenen Dreiecke zu lösen. Die Kinder können dann die Antworten mit bestimmten Farben kombinieren, um das Bild zu dekorieren. Sobald sie die passende Farbe haben, können sie den entsprechenden Teil des Bildes ausmalen.

4. geogebra

Mit den Aktivitäten in Geogebra können die Schülerinnen und Schüler das Sinusgesetz veranschaulichen. Die Schülerinnen und Schüler erstellen verschiedene Dreiecke, indem sie die Punkte auf dem Bildschirm verschieben. Die sechs Werte der Teile des Dreiecks ändern sich, wenn die Punkte verschoben werden. Es gibt viele Möglichkeiten zu erkunden!

5. mapQuest

Nehmen Sie Ihre Stadt mit MapQuest aus der Vogelperspektive auf. Geben Sie den Kindern einen Winkelmesser, eine Karte und die Anleitung. Sie sollen Dreiecke mit nur wenigen vorgegebenen Maßen erstellen und die Entfernungen zwischen den Orten auf der Karte berechnen. Sie müssen genau messen, um die richtigen Entfernungen zu finden.

6. sonnenuhren

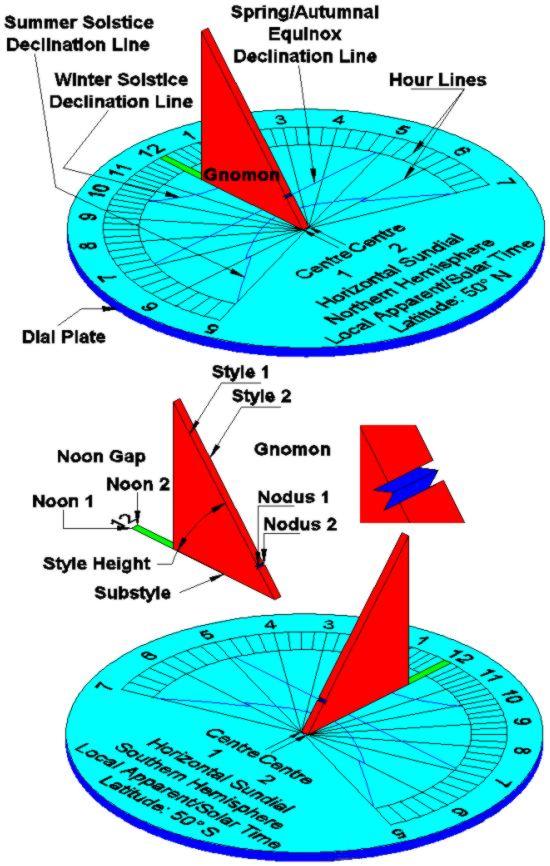
Die Schüler üben, Dreiecke zu messen, um die Länge von skalenförmigen Dreiecken zu berechnen, um die Höhe des Gnomons auf ihren Sonnenuhren zu ermitteln. Sie verwenden die Höhe der Sonne und die Schattenlänge in verschiedenen Breitengraden, um die Länge des Stils zu berechnen.

7. die Fälschung finden

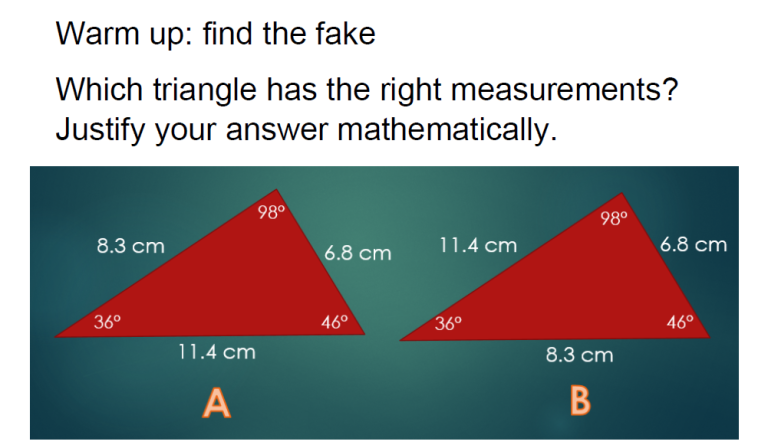
Lassen Sie die Schüler sich bei jedem Winkel vorstellen, dass der Lichtstrahl einer Taschenlampe auf die gegenüberliegende Wand gerichtet ist. Welcher Winkel würde den Kreis mit dem größten Durchmesser auf der gegenüberliegenden Wand ergeben? Der größte Winkel ergibt den größten Durchmesser, so dass die Schüler schließlich feststellen werden, dass B falsch ist.

8. trashketball

Mit einem einfachen Mülleimer und einem Bündel Papier lässt sich eine Rechenaufgabe im Team lösen. Die Kinder lösen die Aufgaben und überprüfen mit Ihnen, ob sie richtig sind. Wenn sie richtig liegen, erhalten sie die Chance, Punkte zu erzielen, indem sie einen Korb machen - markieren Sie den Boden mit Klebeband als 1- und 2-Punkte-Linien.

9. schnitzeljagd

Erstellen Sie eine Reihe von Wortproblemen und hängen Sie sie im Raum auf. Die Schüler müssen die Aufgaben lösen und die richtigen Antworten mit der "vorherigen Antwort", die auf jeder neuen Aufgabe steht, abgleichen. Wenn sie das richtig machen, sollten sie alle Aufgaben lösen und dabei Buchstaben sammeln, um ein Rätsel zu lösen.

10. minigolf

Erforschen Sie die Trigonometrie mit diesem interaktiven Minigolfspiel. Die Kinder müssen die Antworten mit Hilfe des Sinus- und Kosinusverhältnisses berechnen, um dieses lustige Golfspiel richtig spielen zu können. Dies gibt der komplexen Mathematik einen realen Dreh, so dass die Kinder die Anwendung auf den Spaß im Freien sehen können.

11. aufstapeln

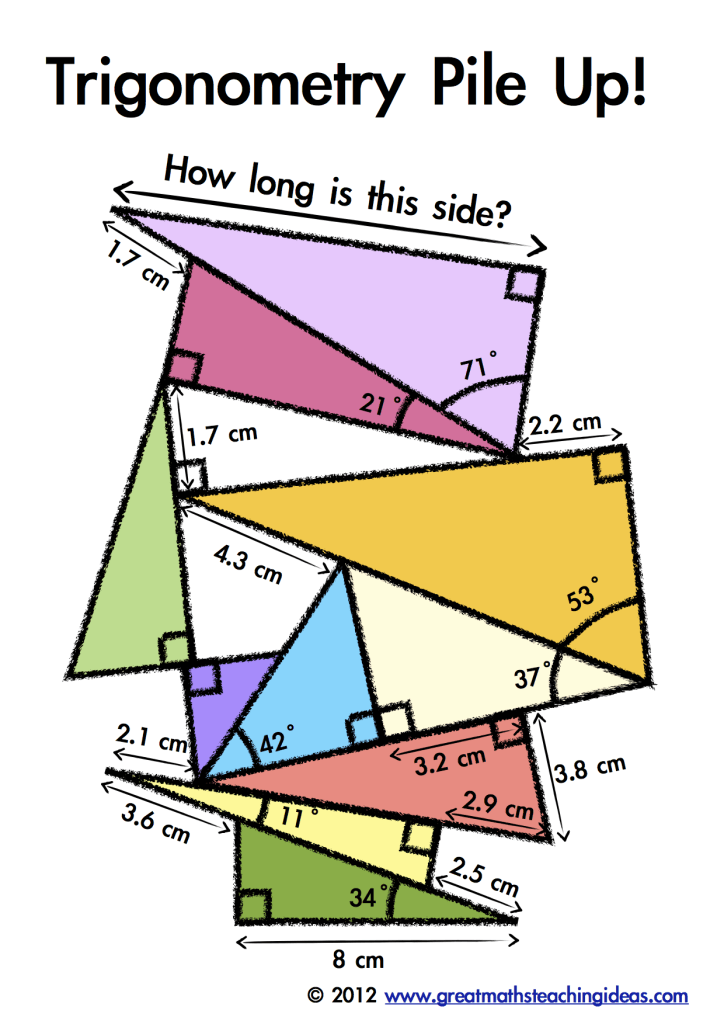
Die Kinder lösen dieses schwierige Rätsel mit Hilfe trigonometrischer Prinzipien, einschließlich Sinus und Kosinus. Sie müssen die gegebenen Informationen nutzen, um die fehlenden Winkel und Seitenlängen zu berechnen. Das Rätsel erfordert mehrere Schritte, verleitet die Kinder aber dazu, ihre eigenen Pile-Ups zu erstellen, die andere lösen sollen.

12. der Trigonometrie-Fluss

Die Schüler wenden ihr Wissen aus der Praxis an, um die Entfernung eines Flusses zu berechnen. Sie arbeiten auch mit der Umrechnung von Einheiten und lernen, wie Ingenieure die Trigonometrie im wirklichen Leben anwenden. Geben Sie den Kindern das Arbeitsblatt, einen Winkelmesser und eine Schnur, um Entfernungen zu schätzen und zu berechnen.

13. zen mathe

Lassen Sie die Schüler Linien auf weißem Papier ziehen, um 10 leere Abschnitte zu erstellen. Berechnen Sie dann die fehlenden Antworten auf jedem Dreieck und ordnen Sie sie einem entsprechenden Muster zu. Verwenden Sie schließlich das Muster, um eine der leeren Stellen auf der Zeichnung auszufüllen.

14. raketenwinkel

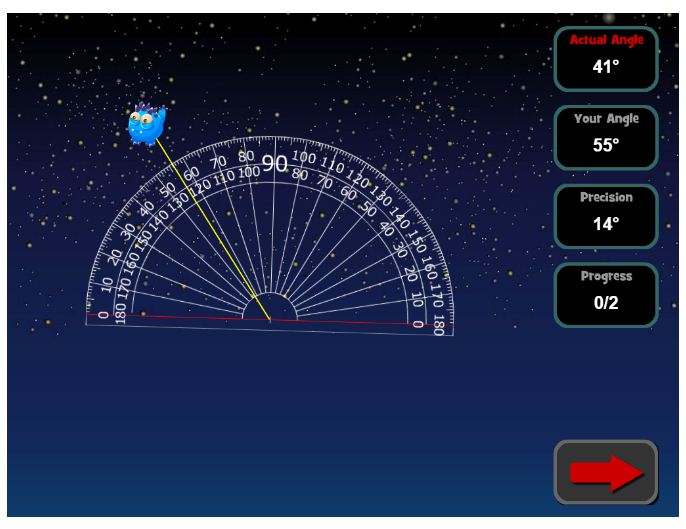
In diesem interaktiven Onlinespiel werden die Kinder zu Kapitänen von Raketenschiffen. Sie berechnen die fehlenden Winkel, um Außerirdische im Weltraum zu finden. Jeder Schüler benötigt einen Winkelmesser, um die Winkel und Formen zu berechnen.

15. die Angry Birds

Ob Sie es glauben oder nicht, Angry Birds hilft Kindern, die Winkel zu visualisieren, die zum Abschießen von Vögeln benötigt werden. Sie lernen trigonometrische Prinzipien, indem sie sich den optimalen Projektilwinkel vorstellen, um ihr Ziel zu treffen. Warum nicht ein zusätzliches Element hinzufügen, indem sie Winkelmesser einbeziehen und sie Dreiecke identifizieren lassen?

16. berufliches Vorstellungsvermögen

Lassen Sie die Schülerinnen und Schüler den Nutzen der Trigonometrie in verschiedenen Berufen untersuchen. Machen Sie ein Brainstorming, in welchen Berufen Dreiecke verwendet werden und Entfernungen berechnet werden müssen. Lassen Sie die Kinder dann recherchieren, um ihre Vorhersagen zu bestätigen.

17 Erstellen Sie Ihr eigenes

Fordern Sie die Kinder auf, ein eigenes anspruchsvolles Wortproblem zu entwerfen und mit Illustrationen zu versehen, um reale Anwendungen zu zeigen. Lassen Sie sie das Problem einzeln lösen und fordern Sie dann andere auf, die Antwort zu finden oder das Problem zu lösen und ein Poster zu erstellen, um ihr Wissen zu präsentieren.

18. trigonik

Fördern Sie Ihre kinästhetischen Fähigkeiten mit diesem komplexen und unterhaltsamen Brettspiel. Zwei Spieler treten gegeneinander an, um ihre Zwillingsplättchen durch Würfeln und Lösen von Aufgaben durch das Spielbrett zu bringen. Auf den Würfeln sind verschiedene SIN- und COS-Optionen abgebildet, wobei die Spieler ihre Plättchen entlang eines Kreises positionieren.

19. punkt-zu-punkt

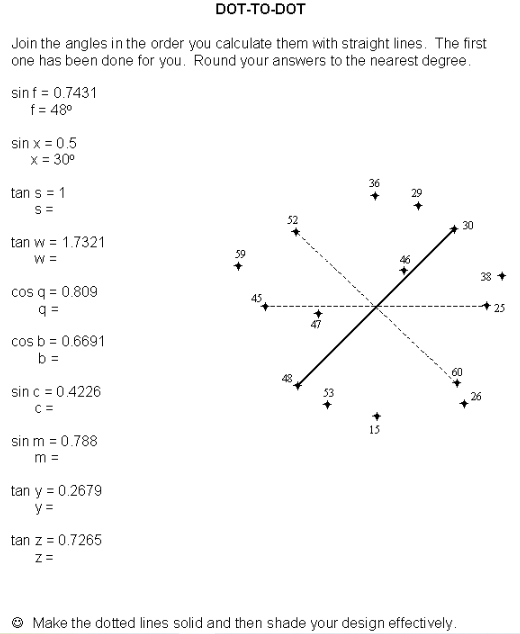
Mit dieser kreativen Problemlösung wird das altbekannte Punkt-zu-Punkt-Verfahren aufgewertet: Die Kinder müssen die Antworten auf mehrere trigonometrische Aufgaben finden, um herauszufinden, welche beiden Liniensegmente als nächstes in ihrem Rätseldiagramm verbunden werden sollen.

20. 3D-Berechnungen

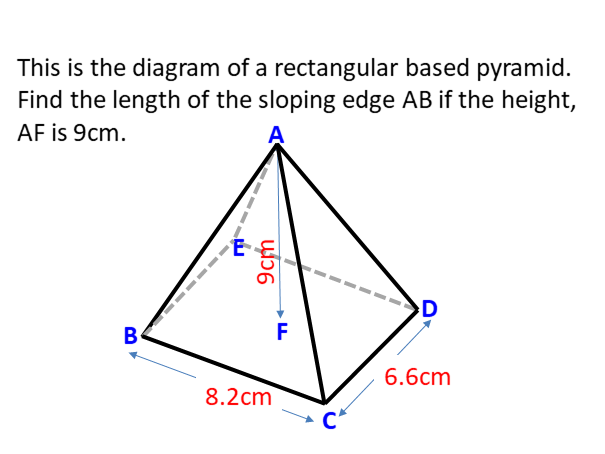
Fortgeschrittene Schüler können beginnen, Mathematik in 3D-Formen zu visualisieren. Arbeiten Sie mit diesen Aufgaben, um eine erweiterte Version der Trigonometrie unter Verwendung des Gesetzes von Sinus und Kosinus zu demonstrieren. Die Kinder müssen die fehlenden Winkel und Seitenmaße bestimmen, um die 3D-Form zu lösen.

21 Videos aus der realen Welt

Hören Sie sich an, wie bekannte Fachleute aus verschiedenen Berufen darüber sprechen, wie sie Mathe täglich in ihrem Beruf einsetzen. Anschließend können die Kinder diese Online-Spiele und -Probleme selbst ausprobieren. Von Mathe im Basketball bis hin zu Mathe bei Spezialeffekten - die Kinder werden von all den realen Anwendungen ihres Studiums begeistert sein!

22. virtuelle Manipulatoren

Die National Library of Virtual Manipulatives bietet eine Vielzahl von Spielen für verschiedene Niveaus an, die den Kindern helfen, Mathematik auf eine neue Art und Weise zu visualisieren und kinästhetisch mit den Problemen umzugehen, wie z. B. die Messung der Entfernung zwischen Weltstädten.