2차 인수분해는 주요 수학 주제이며 2차 방정식을 풀고 복잡한 표현을 단순화하는 데 필수적입니다. 이 중요한 학습 영역은 학생들이 물리학, 공학 및 금융 분야에서 더 많은 연구를 하고자 하는 경우에도 매우 중요합니다. 학급 활동에 인수분해 이차를 포함하는 매력적인 방법을 찾는 것은 어려운 작업이 될 수 있습니다. 우리는 학급을 흥미롭게 만들 13가지 재미있는 인수분해 2차 활동을 발견했습니다. 살펴보겠습니다.

1. 삼항식 소인수 소책자

종이 한 장을 삼등분으로 접어서 만드는 간단한 소인수 소책자입니다. 학생들에게 다채로운 표지를 만든 다음 최대공약수 인수분해, 제곱차 인수분해, a=1인 삼항식 인수분해, a > 1, 4항을 인수분해.

2. Quadratic Chain Link 활동

이 슈퍼 활동은 수학 학생들의 인수분해 기술을 테스트합니다! 각 학생에게 완료할 체인 2개를 줍니다. 이것이 완료되면 체인을 함께 결합하여 이 체인을 만들 수 있습니다. 이것들은 디스플레이에 멋지게 보이며 학습 전반에 걸쳐 참조할 수 있습니다.

3. Factoring Puzzle Laminated Sheet

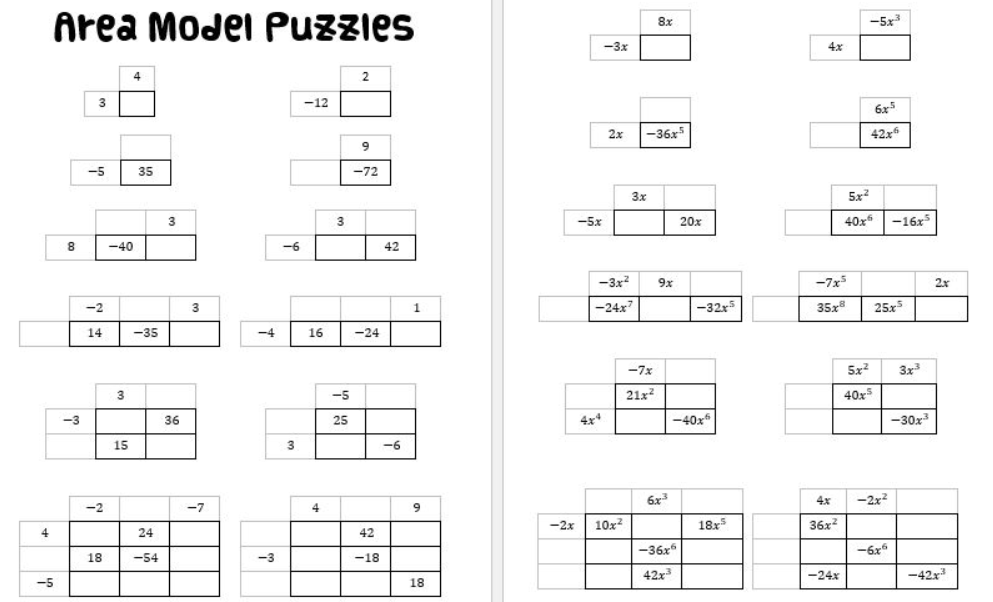
이 퍼즐은 단원이 끝난 후 이해도를 확인하기에 좋습니다. 학생들은 검은색 인수분해 질문을 완료해야 합니다.마커를 선택한 다음 파트너와 교체하여 표시합니다.

4. 색칠 활동

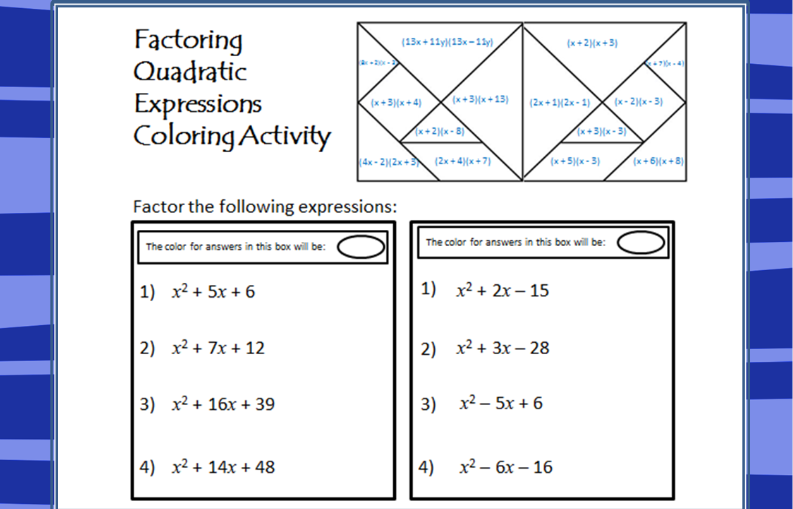
이 매력적인 활동을 통해 학생들은 수학 수업에서 창의력을 발휘할 수 있습니다! 색상 키를 만들고 키에 할당된 색상에 따라 다른 이차식의 색상을 지정해야 합니다. 이것은 눈에 띄는 패턴을 만듭니다.

5. 핸디 박스 방법

이 핸디 비디오는 학생들에게 이차식을 인수분해할 때 사용할 수 있는 핸디 박스 인수분해 방법을 안내합니다. 이를 통해 학생들은 가치 있는 인수분해 연습을 하고 다양한 방법을 실험할 수 있습니다.

6. 2차 카드 정렬

이 카드 정렬 활동은 학생들이 특별한 경우가 있는 다항식을 인수분해하는 과정을 안내합니다. 학생들은 그리드의 각 다항식을 인수분해하여 그것이 완전제곱삼항식인지, 제곱의 차이인지, 아니면 둘 다인지 알아내야 합니다. 그런 다음 올바른 팩터링 카드를 사각형에 넣어야 합니다.

7. 인수분해 이차 연습 활동

이 워크시트의 각 페이지에는 다항식이 포함되어 있습니다. 페이지 하단에는 학생들이 잘라낼 요소가 있습니다. 그런 다음 올바른 요소를 찾아 올바른 위치에 붙여 각 문제를 해결해야 합니다.

8. Quadratics Codebreaker

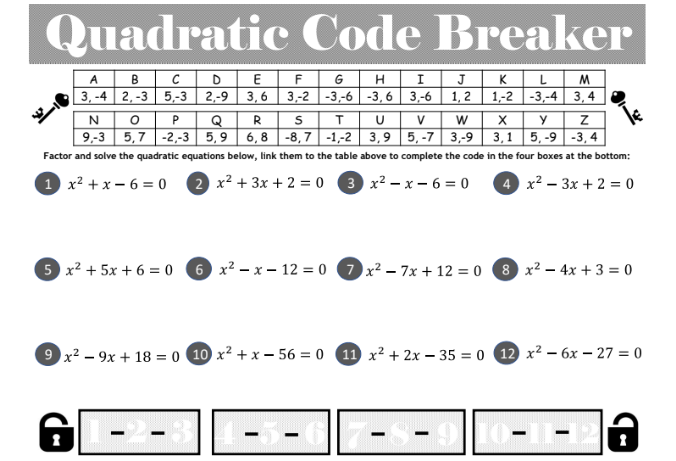
이 퍼즐은 학생들이 이차방정식을 인수분해하고 풀고 키와 일치시키는 과정을 안내합니다. 코드에 대한 답을 공개합니다.그런 다음 학생들은 코드가 올바른지 확인하여 답변을 확인합니다.

9. 인수분해 삼항식 흐름도

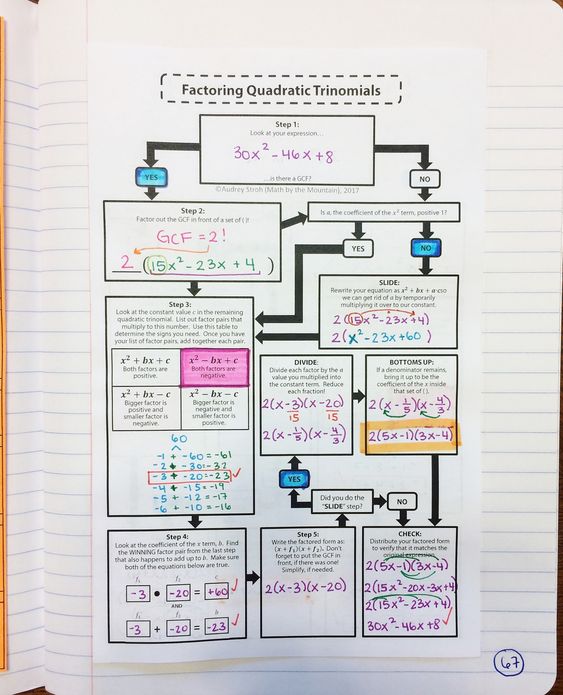
이 흐름도를 통해 학생들은 모든 2차 삼항식을 풀 수 있습니다. 차트를 참조 시트로 사용할 때 어려운 인수분해 질문을 쉽게 풀 수 있어야 합니다. 먼저 화이트보드에 차트를 모델링합니다. 그런 다음 학생들은 자신의 책에서 자신의 순서도를 만들 수 있습니다. 원하는 대로 자신만의 색상과 디테일을 추가합니다.

10. 인수분해 전 퍼즐

이 인수분해 퍼즐 워크북에서 학생들은 빠진 숫자를 채우면서 많은 인수분해 연습을 할 수 있습니다. 이들은 2차 방정식을 인수분해하는 것과 동일한 사고 과정을 사용합니다.

11. 인수분해 전 활동

이 활동에서 학생들은 이차식 인수분해에 필요한 몇 가지 필수 기술을 연습합니다. 학생들은 각 2차 방정식에 2개의 이항식을 일치시켜야 합니다. 보드의 올바른 위치에 배치합니다.

12. Polynomials Foldable

2차 인수분해는 학생들이 마스터하기 까다로운 기술이 될 수 있습니다. 접을 수 있는 팩토링을 통해 학생들은 자신의 속도에 맞춰 질문을 풀고 필요한 경우 다시 참조할 수 있도록 통합 문서에 붙일 수 있습니다.

13. 팩터링을 통한 매칭

화이트보드나 대형 포스터 보드에 팩터링하고 싶은 표현을 여러 개 만듭니다. 다음으로 색인 카드에 식의 분해된 형식을 적습니다.플러스 시트에 포함되지 않은 일부. 그런 다음 학생들은 분해된 표현식을 올바른 원래 표현식과 일치시켜야 합니다.